ニューラルネットワークは、人工知能(AI)の根幹をなす技術の一つです。近年、機械学習や深層学習の発展に伴い、ニューラルネットワークはますます注目を集めています。本記事では、ニューラルネットワークの基本概念から歴史、数式、Pythonでの実装例まで、わかりやすく解説していきます。
ニューラルネットワークとは
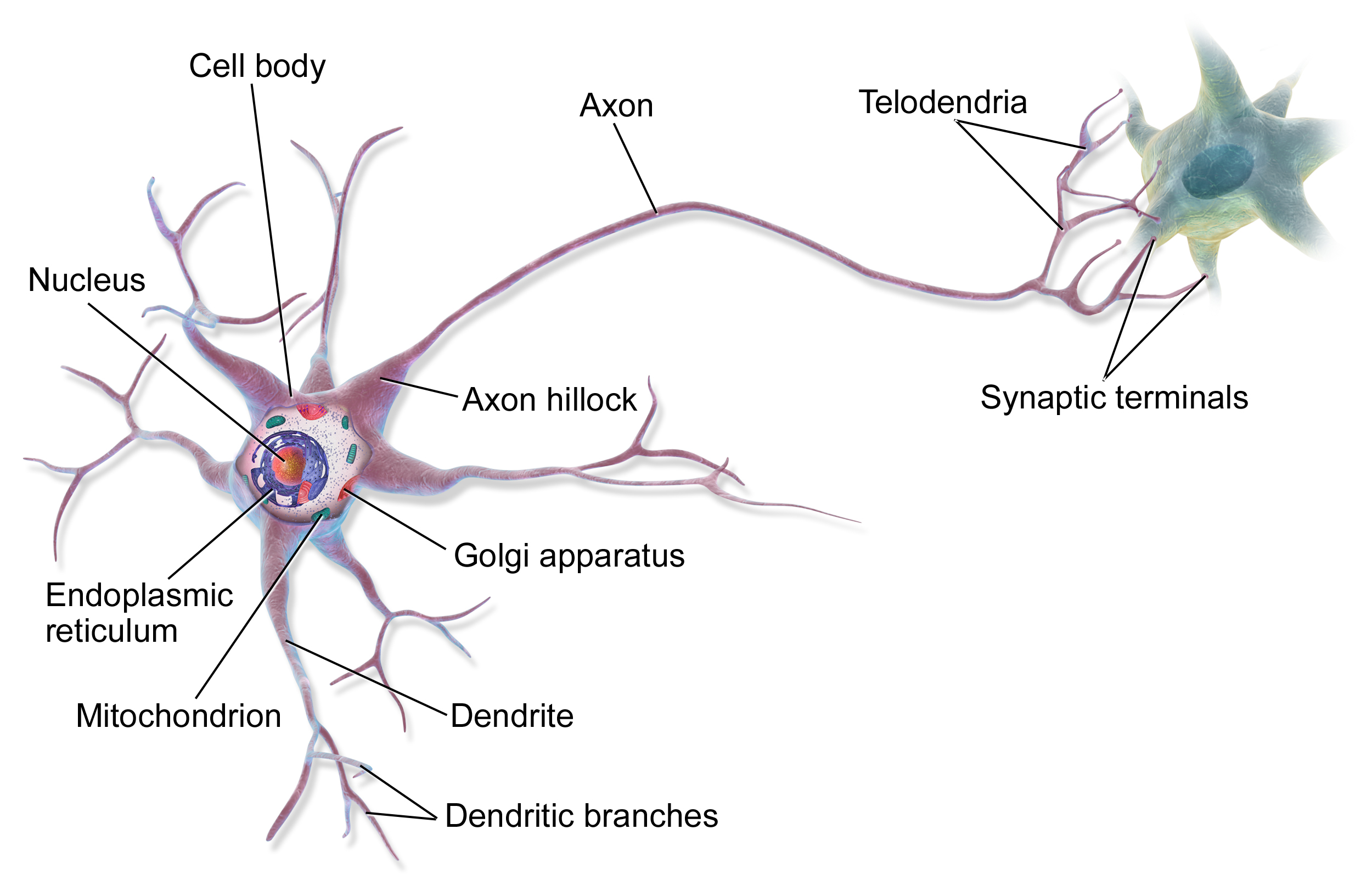
ニューラルネットワークは、人間の脳内にある神経細胞(ニューロン)のネットワークを数学的にモデル化したものです。複数の層(入力層、隠れ層、出力層)から構成され、各層のニューロン間が重みづけされた接続で結ばれています。この構造により、ニューラルネットワークは複雑な関数を学習し、パターン認識や予測などのタスクを実行できます。
ニューラルネットワークの構成要素
ニューラルネットワークは、複数の層から構成されています。各層の役割と特徴について、詳しく見ていきましょう。
入力層
入力層は、ニューラルネットワークにデータを入力する役割を担っています。入力層のニューロンの数は、入力データの次元数に対応します。例えば、28×28ピクセルの画像を入力する場合、入力層のニューロンの数は784(=28×28)になります。
隠れ層
隠れ層は、入力層と出力層の間に位置する層です。隠れ層のニューロンは、入力層からの信号を受け取り、非線形変換を施して、出力層に信号を送ります。隠れ層の数とニューロンの数は、タスクの複雑さや用いるデータの特性に応じて設定します。
隠れ層で用いられる活性化関数は、非線形性を導入するために重要な役割を果たします。代表的な活性化関数として、以下のようなものがあります。
- シグモイド関数:\(f(x) = \frac{1}{1 + e^{-x}}\)
- tanh関数:\(f(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}\)
- ReLU(Rectified Linear Unit)関数:\(f(x) = \max(0, x)\)
近年、ReLU関数が広く用いられています。ReLU関数は、勾配消失問題を緩和し、ニューラルネットワークの学習を高速化するという利点があります。
出力層
出力層は、ニューラルネットワークの最終層であり、タスクに応じた出力を生成します。出力層のニューロンの数は、タスクの種類によって異なります。例えば、二値分類のタスクでは、出力層のニューロンの数は1になります。多クラス分類のタスクでは、出力層のニューロンの数はクラスの数に対応します。
出力層で用いられる活性化関数は、タスクの種類によって異なります。二値分類では、シグモイド関数が用いられることが多いです。多クラス分類では、ソフトマックス関数が用いられることが多いです。ソフトマックス関数は、出力を確率分布に変換します。
ニューラルネットワークの学習
ニューラルネットワークの学習は、教師あり学習の一種です。教師データ(入力データとそれに対応する正解ラベル)を用いて、ニューラルネットワークのパラメータ(重みとバイアス)を調整します。学習の目的は、教師データに対する予測誤差を最小化することです。
誤差関数
ニューラルネットワークの学習では、予測値と正解ラベルの差を定量化する誤差関数を定義します。代表的な誤差関数として、以下のようなものがあります。
- 平均二乗誤差(Mean Squared Error, MSE):\(E = \frac{1}{2N}\sum_{i=1}^N(y_i – t_i)^2\)
- クロスエントロピー誤差(Cross Entropy Error):\(E = -\frac{1}{N}\sum_{i=1}^N\sum_{k=1}^Kt_{ik}\log y_{ik}\)
ここで、\(N\)はデータの数、\(y_i\)は予測値、\(t_i\)は正解ラベル、\(K\)はクラスの数です。
最適化アルゴリズム
ニューラルネットワークの学習では、誤差関数を最小化するためのパラメータ更新を行います。パラメータ更新には、最適化アルゴリズムを用います。代表的な最適化アルゴリズムとして、以下のようなものがあります。
- 確率的勾配降下法(Stochastic Gradient Descent, SGD)
- モーメンタム法(Momentum)
- AdaGrad(Adaptive Gradient)
- Adam(Adaptive Moment Estimation)
これらの最適化アルゴリズムは、勾配降下法をベースとしながら、学習率の適応的な調整や、パラメータ更新の加速などの工夫を取り入れています。
過学習の防止
ニューラルネットワークは、柔軟性が高く、表現力が豊かなモデルです。その一方で、訓練データに過剰に適合してしまう過学習(overfitting)が起こりやすいという問題があります。過学習を防止するために、以下のような手法が用いられます。
- 正則化(Regularization):パラメータの大きさにペナルティを課すことで、モデルの複雑さを制御します。L1正則化とL2正則化が代表的です。
- ドロップアウト(Dropout):学習時に、ランダムにニューロンを無効化することで、モデルの過剰な適合を防ぎます。
- アーリーストッピング(Early Stopping):検証データに対する誤差が増加に転じた時点で学習を打ち切ることで、過学習を防ぎます。
ニューラルネットワークの発展の歴史をより詳しく
ニューラルネットワークの歴史は、1940年代にさかのぼります。以下では、ニューラルネットワークの発展の主要なマイルストーンを詳しく見ていきます。
1943年:McCulloch-Pittsニューロン
Warren McCullochとWalter Pittsは、1943年に「A Logical Calculus of the Ideas Immanent in Nervous Activity」という論文を発表し、ニューロンの数理モデルを提案しました。このモデルは、McCulloch-Pittsニューロンと呼ばれ、ニューラルネットワークの基礎となりました。
1958年:パーセプトロン
Frank Rosenblattは、1958年に「The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain」という論文を発表し、パーセプトロンを開発しました。パーセプトロンは、単層のニューラルネットワークであり、線形分離可能な問題を学習することができました。
1969年:パーセプトロンの限界
Marvin MinskyとSeymour Papertは、1969年に「Perceptrons」という本を出版し、パーセプトロンの限界を指摘しました。彼らは、パーセプトロンがXOR問題のような非線形分離問題を解けないことを示しました。この指摘により、ニューラルネットワークの研究は一時的に停滞しました。
1986年:誤差逆伝播法
David RumelhartとGeoffrey Hintonらは、1986年に「Learning representations by back-propagating errors」という論文を発表し、誤差逆伝播法(バックプロパゲーション)を提案しました。誤差逆伝播法は、多層ニューラルネットワークの学習を可能にし、ニューラルネットワークの研究が再び活性化するきっかけとなりました。
1989年:畳み込みニューラルネットワーク(CNN)
Yann LeCunらは、1989年に「Backpropagation Applied to Handwritten Zip Code Recognition」という論文を発表し、畳み込みニューラルネットワーク(CNN)を提案しました。CNNは、画像認識のタスクで高い性能を示し、現在に至るまで広く用いられています。
1997年:長短期記憶(LSTM)
Sepp HochreiterとJürgen Schmidhuberは、1997年に「Long Short-Term Memory」という論文を発表し、長短期記憶(LSTM)を提案しました。LSTMは、リカレントニューラルネットワーク(RNN)の一種であり、長期的な依存関係を学習することができます。LSTMは、自然言語処理や時系列データ解析で広く用いられています。
2006年:深層信念ネットワーク(DBN)
Geoffrey Hintonらは、2006年に「A fast learning algorithm for deep belief nets」という論文を発表し、深層信念ネットワーク(DBN)を提案しました。DBNは、複数の制限付きボルツマンマシン(RBM)を積層したモデルであり、事前学習とファインチューニングによって学習します。DBNは、深層学習の発展に大きく貢献しました。
2012年:ImageNetの画像認識コンペティション
2012年に開催されたImageNetの画像認識コンペティションで、Geoffrey Hintonらが提案した深層畳み込みニューラルネットワーク(CNN)が高い精度を達成しました。このできごとを契機に、深層学習が脚光を浴び、ニューラルネットワークの研究が再び活性化しました。
2017年:Transformer
Ashish Vaswaniらは、2017年に「Attention Is All You Need」という論文を発表し、Transformerを提案しました。Transformerは、自然言語処理のタスクで高い性能を示し、現在に至るまで広く用いられています。
以上が、ニューラルネットワークの発展の主要なマイルストーンです。ニューラルネットワークの研究は、長い歴史を持ちながらも、現在も活発に行われており、今後のさらなる発展が期待されています。
ニューラルネットワークの数式表現
ニューラルネットワークを数式で表現すると、以下のようになります。
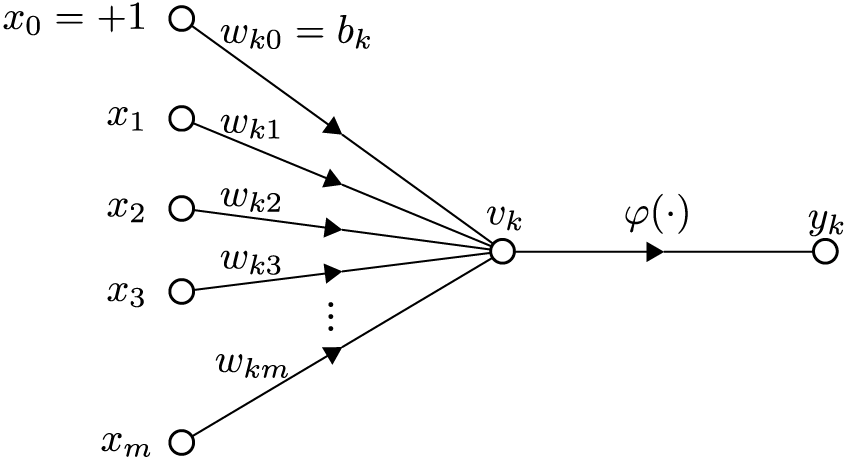
入力層のニューロンの出力を \(x_i\)、隠れ層のニューロンの出力を \(h_j\)、出力層のニューロンの出力を \(y_k\) とします。また、入力層から隠れ層への重みを \(w_{ij}\)、隠れ層から出力層への重みを \(w_{jk}\) とします。
隠れ層のニューロンの出力は、以下の式で計算されます。
$$h_j = f(\sum_i w_{ij} x_i + b_j)$$
ここで、\(f\) は活性化関数、\(b_j\) はバイアス項です。
出力層のニューロンの出力は、以下の式で計算されます。
$$y_k = f(\sum_j w_{jk} h_j + b_k)$$
ニューラルネットワークの学習では、教師データを用いて、重みとバイアスを調整します。代表的な学習アルゴリズムとして、誤差逆伝播法があります。
Pythonでのニューラルネットワークの実装例
Pythonを使って、簡単なニューラルネットワークを実装してみましょう。基本的には、ライブラリを利用して実装を行います。
Pytorchの場合
import torch
import torch.nn as nn
import torch.optim as optim
# ニューラルネットワークの定義
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(784, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
# モデルの初期化
model = Net()
# 損失関数とオプティマイザの定義
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# 訓練ループ
for epoch in range(10):
for inputs, labels in train_loader:
inputs = inputs.view(-1, 784)
outputs = model(inputs)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()Tensorflowの場合
import tensorflow as tf
# ニューラルネットワークの定義
model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu', input_shape=(784,)),
tf.keras.layers.Dense(10)
])
# モデルのコンパイル
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
# モデルの訓練
model.fit(x_train, y_train, epochs=10, batch_size=32)Kerasの場合
from tensorflow import keras
# ニューラルネットワークの定義
model = keras.Sequential([
keras.layers.Dense(128, activation='relu', input_shape=(784,)),
keras.layers.Dense(10, activation='softmax')
])
# モデルのコンパイル
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# モデルの訓練
model.fit(x_train, y_train, epochs=10, batch_size=32)まとめ
ニューラルネットワークは、人工知能の基礎となる技術であり、近年の深層学習の発展に大きく貢献しています。本記事では、ニューラルネットワークの基本概念、歴史、数式表現、Pythonでの実装例について解説しました。ニューラルネットワークを理解することは、AIの原理を学ぶ上で重要な一歩となるでしょう。今後も、ニューラルネットワークの研究が進展し、より高度なAIが実現されることが期待されます。今大いに流行っている生成AIもこの技術の進化の賜物ですね。






コメント